How is emission calculated for Miners? Emission is derived from the incentive calculated by Yuma Consensus.

1. Validators test miners, and create a ranked list of each miner (weights). These weights are regularly delivered to the consensus engine.
   1. These are stored in a 2D matrix - each row is the UID of the validator placing weights, and each column is the UID of the miner. (A visual representation of the weights can be found for each subnet on taostats: Subnet 19 Miner weights .
2. These weights are used to calculate incentive and consensus - how well do the validators agree on scoring?
3. The incentive score is made by a weighted average of validator weights. Weights placed by validators with higher amounts of delegation of tao are given higher weight in the incentive score. Validators that are out of consensus (a high deviation from the consensus score) may have their weight reduced further.

Incentive

The incentive score for a subnet scores how well miners are performing in relation to other miners. The sum of incentive scores in a subnet is 1.

Emission

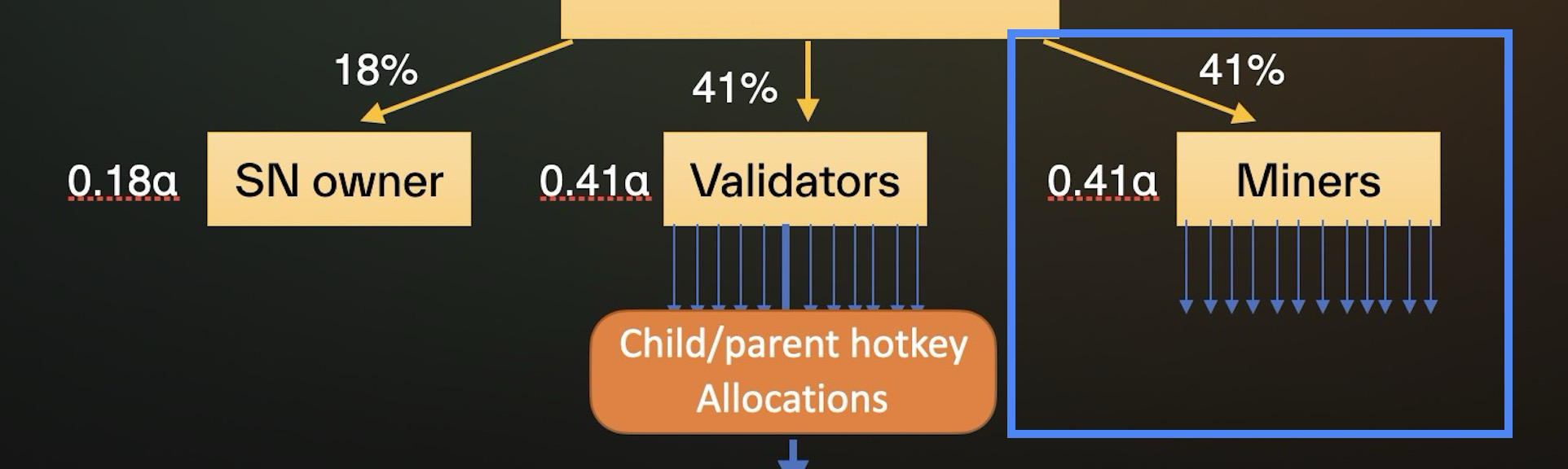
The miner emission score is how much tao is awarded to the miner each epoch. (An epoch is 360 blocks)

📘

Emission math example

A subnet receives 0.05 tao per block.

In 1 epoch - 0.05*360 = 18 tao.

Miners receive 41% of the subnet' emissions. 18*.41 = 7.38 tao.

Miner 19 has incentive of 0.006. 7.38*0.006 = 0.04428 tao per epoch.

Miner 19 has 0.04428 emission

Emission is calculated every epoch, but is awarded once every 7200 blocks. This can mean that emission is delivered to your hotkey after your miner is deregistered.

Daily Rewards

On taostats, the daily rewards is calculated by multiplying emission *20 (There are ~20 epochs in 24 hours.)

Math

We can extract the weights, consensus, and incentive scores from the network, and look at how they interact.

Let's grab the data for Subnet 18, miner 191.

import bittensor as bt

#who we are interested in
subnet_number = 18
miner_uid = 191

#validator parameters:
#we need to find the rows for where validators have placed weights.
#find the rows by lookin in the stake vector for rows with large delegation
min_stake = 22000
validators = []
total_stake = 0
counter =0

#load the data from the network
subnet = bt.metagraph( netuid = subnet_number, lite = False)
subnet_weights = subnet.W
subnet_stake = subnet.S
subnet_consensus = subnet.C
subnet_incentive = subnet.I


#loop through all of the UIDs.
#if there is a large amount of stake - we have a validator
#grab the weight placed for the miner_uid
for neuron in subnet_stake:
    stake = neuron.item()
    if stake > min_stake:
        weight = subnet_weights[counter][miner_uid]
        print(f"validator {counter}: Weight {weight}")
        
    counter += 1
    
#now grab consensus and incentive
print(f"consensus: {subnet_consensus[miner_uid]}") 
print(f"incentive: {subnet_incentive[miner_uid]}") 

validator 21: Weight 0.0022598521318286657
validator 63: Weight 0.0014278064481914043
validator 77: Weight 0.002753422362729907
validator 104: Weight 0.00243220292031765
validator 120: Weight 0.0
validator 132: Weight 0.001061580260284245
validator 133: Weight 0.003077547997236252
validator 139: Weight 0.003447300987318158
validator 145: Weight 0.0017241350142285228
validator 160: Weight 0.0019509864505380392
validator 171: Weight 0.0030758935026824474
validator 175: Weight 0.0037663523107767105
validator 180: Weight 0.001641291193664074
validator 181: Weight 0.0024577134754508734
validator 187: Weight 0.0022174983751028776
validator 188: Weight 0.0017739878967404366
validator 190: Weight 0.0033894709777086973
validator 194: Weight 0.004710848908871412
validator 230: Weight 0.0024577134754508734
validator 232: Weight 0.0021844268776476383
validator 236: Weight 0.0030592582188546658
validator 246: Weight 0.0021754945628345013
consensus: 0.0021820401307195425
incentive: 0.002151522086933255

The code calls the Chain and asks for all of the validator weights. The output is a formatted list with the weight from each validator. In the response, we can see on line 5 that validator 120 placed no weight. This score will be removed by the consensus engine, and the VTrust for the validator will be reduced.

📘

VTrust for validator 120

The code below queries the chain for the VTrust for validators 120, 232 and 236. The number is reported in a Tensor:

120: 44.5%
232: 93.9%
236: 89.6%

print(subnet.Tv[120])
print(subnet.Tv[232])
print(subnet.Tv[236])

tensor(0.4450)
tensor(0.9391)
tensor(0.8962)

At 44.5% Vtrust, validator 120 will begin to see lower emissions.

The overall consensus is 0.00218, and looking at the weights placed by each validator - we can see that most of the validators are close to that score. The overall incentive is right around the consensus (slightly lower) at 0.00215

Charting Weights and Consensus

The code below draws a red dotted line indicating the consensus weight. Each validator's weight is shown by a blue dot.

import matplotlib.pyplot as plt


# Unpack the points into two lists: xs and ys
xs, ys = zip(*weights)

# Create a scatter plot
plt.scatter(xs, ys)

# Add a horizontal line at y = consenus
plt.axhline(y=subnet_consensus[miner_uid], color='r', linestyle='--')

# Set the labels for the axes
plt.xlabel('Validator UID')
plt.ylabel('Weight')

# Set the title of the plot
plt.title(F'weights and consensus for miner {miner_uid} in subnet {subnet_number}')

# Show the plot
plt.show()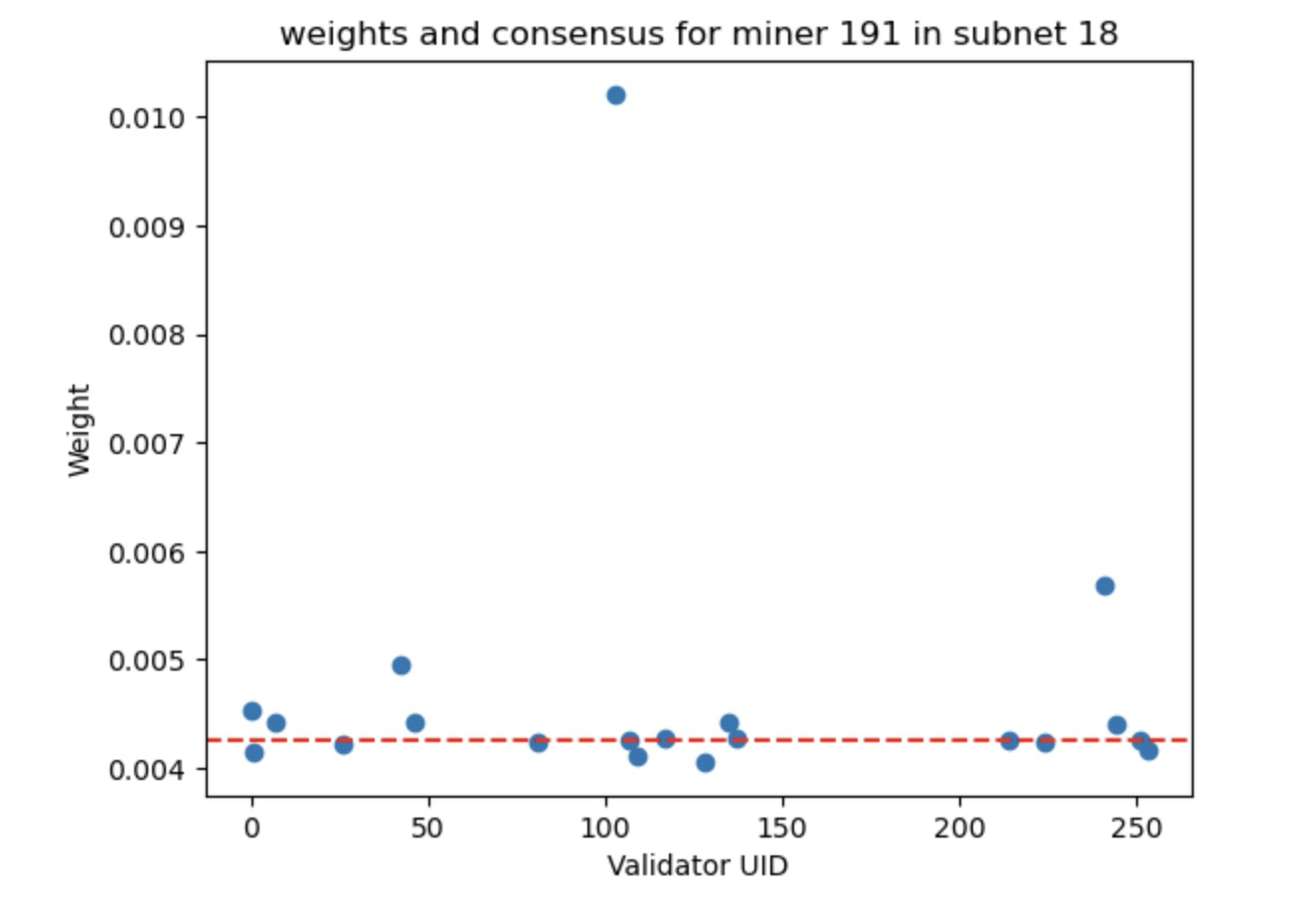

Validator 103 is the point at the top of the graph, and out of consensus with the others - all much closer to the consensus line. The weight posted by Validator 103 will not be included (or its weight drastically reduced) as it is out of consensus.